
Electronic english version since 2022 |
The newspaper was founded in November 1957
| |
From childhood intuition to high-level research
I loved physics in elementary school (though at that time I didn't yet know that it was physics). In my yard, there was a children's standing carousel in the shape of the Russian letter "Ф" where my friends and I loved to spend time after school. The centre of the carousel was fixed and dug into the ground and the carousel itself spun around the centre. The carousel was heavy and in order to spin on it, small and light girls needed to put in a lot of effort (they had to cling to it and push off the ground with their feet to speed up the rotation). At some point, I realized that if I lightly pushed off and began to move towards the centre along the crossbar of the carousel, the carousel began to rotate much faster. "Wow, how great," I thought, "Now, I won't have to put in a lot of effort to push my feet off the ground!" Thus, I intuitively applied the laws of physics that describe rotational motion to my life back in elementary school, not knowing the formulae and the fact that the speed of rotation of the carousel depends on the position of the masses. A lot of time has passed since then and today, I am engaged in nuclear physics, studying various characteristics of nuclei, including their rotation. Is it a coincidence?

After elementary school, I accidentally entered the physics and mathematics lyceum, where I studied until the 11th grade. I remember well the moment when I started learning physics in the 7th grade and I eagerly tried to absorb all the information that the teachers gave in class. Every six months, starting from the 7th grade, we took exams, mathematics and Russian were compulsory, the rest of the subjects were chosen by the student himself. And every six months, I took a physics exam that I passed successfully. In the 9th grade, we were assigned to specialized training. Of course, I went to physics and mathematics, where I studied natural science subjects with great desire. My love for physics was due to the fact that all the laws and rules were applicable in everyday life. For example, while studying the topic "Vibrations", I realized the following rule: "If you carry a full cup of tea, you need to walk quickly, otherwise, the vibrations of the surface of the liquid and your movement will "add up" that will cause a resonance and the tea will be spilled on the floor. Have you already spilled your tea? Don't despair, there is a life hack for this too - just smear the stain to increase its area, thereby speeding up evaporation!" Miracles? No, physics!
Of course, I really liked school physics, but in high school, the Olympiad movement took hold of me. I successfully took part in almost all Olympiads (they were held almost every weekend) in physics, mathematics and even cryptography and during the holidays, my classmates and I went to physics and mathematics schools that were held on the basis of children's camps.
Of course, my physics teachers played a big role in my development that were able to make their students fall in love with this subject and create a favorable atmosphere for development. Already in those years, I began to think about how important a favorable climate in a team is that promotes effective cooperation between young people and leading scientists. At present, I am a third-year graduate student at the Dubna State University in the area of "Theoretical Physics" and almost 10 years, since graduating from the lyceum, I have constantly studied physics. I have also been working in my specialty for the eighth year at the Bogolyubov Laboratory of Theoretical Physics. Since this year, I have been a representative of the Association of Young Scientists and Specialists in my laboratory and have been widely involved in creating that very friendly creative atmosphere for effective cooperation between young employees of various departments, services and laboratories. I am convinced that it contributes not only to professional, but also to personal growth of employees.
Of course, in parallel with my studies at the university, I am engaged in scientific activities. Starting from the third year of her bachelor's degree, I have worked at BLTP as a laboratory assistant, on the basis of which I wrote my bachelor's thesis "Investigation of heavy nuclei based on the collective Hamiltonian" under the supervision of Elena Kolganova. Our further joint work was carried out in the master's programme, the result of which was the master's thesis "Investigation of the chain of Mo isotopes based on a collective model".
In graduate school, I changed my research area and today, I work under the supervision of Valentin Nesterenko. We study low-energy states of deformed nuclei within the framework of a self-consistent method of chaotic phase approximation with Skyrme forces. As mentioned at the beginning, the rotation of bodies has interested me since childhood and currently, I study the rotational characteristics of deformed nuclei.
During the first two years of graduate school, I was extensively involved in studying the behavior of the moment of inertia of light, highly deformed nuclei 24Mg and 20Ne. Our research shows that the moment of inertia of these nuclei behaves non-standardly: first, it increases with increasing deformation to the equilibrium value and afterwards, begins to decrease sharply (Fig. 1a, 1b). This atypical "decrease" in the moment of inertia in these nuclei became the subject of our research. In our paper, we assume that this behavior of the moment of inertia is explained by shell effects, the influence of pairing and the restructuring of the single-particle spectrum of light, highly deformed 24Mg and 20Ne.

Fig. 1(a, b). Dependence of the moment of inertia of the nucleus J on the deformation of the nucleus β for 24Mg and 20Ne, calculated in three approaches: ATDHF - moment of inertia in the adiabatic approximation (microscopic model of the nucleus), RB - solid-state moment of inertia (macroscopic model of the nucleus), HD - hydrodynamic moment of inertia (macroscopic model of the nucleus). βexp - experimental deformation, black arrow marks the theoretically calculated deformation of the core.
We analyzed the results in two approaches: based on macroscopic and microscopic models. As macromodels, we considered the core as a solid body (Rigid Body, or RB) and as a liquid drop (Liquid Drop, or LD). Macroscopic solid and hydrodynamic moments of inertia depending on the core deformation β are presented by the following formulas:
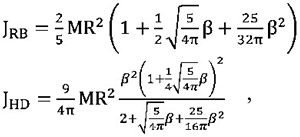
where M is the mass number, R is the radius.
It is obvious that macromodels predict only an increase in the moment of inertia of the core with increasing its deformation.
Micromodels allow for a "decrease" in the moment of inertia with increasing deformation β. As an example of such a micromodel, the moment of inertia calculated in the case of the adiabatic approximation (Adiabatic time-dependent Hartree-Fock, ATDHF) is presented in Figures 1a and 1b: in the experimental value of the equilibrium deformation bexp, the moment of inertia begins to decrease sharply. This behavior of the moment of inertia is also supported by the Inglis-Belyaev (IB) and Thoules-Valatin (TV) micro-approaches, in which the moment of inertia depends directly proportionally on the matrix element and inversely depends on the energy difference between the two levels (it means that a large energy gap is produced between two single-particle levels near the Fermi surface, that is why these levels are far from each other and therefore, weakly interact).
The good news in this paper is that the experimental data support our research at low angular momentum: I=4-6 for 24Mg and I=2-4 for 20Ne.
Of course, this paper can be complemented by using other microscopic approaches, such as the method of antisymmetric molecular dynamics (Antisymmetrized Molecular Dynamics, or AMD). It is also desirable to study the impact of the effects of medium field, clustering, rotation and γ-strain on the behavior of the moment of inertia.
Today, Valentin Nesterenko and I carry out research on deformed nuclei. At present, we study the 250-260No chain, namely, we study the low-lying spectrum of these nuclei and its characteristics. The chain of Nobelium isotopes, like most nuclei in this area, has been poorly studied experimentally that allows theorists to express their assumptions and make predictions regarding certain characteristics of these nuclei. We will work on the analysis of low-lying states of Nobelium isotopes in future that will allow both theorists and experimenters to work together to achieve high results.
Mariya MARDYBAN